The aim is to find a fast method to test TRUE/FALSE if two line segments intersect within their own lengths
If possible, the intersection point should also be returned.
There are lots of ways to do this involving matrices, linear algebra and vectors. This method attempts to use the minimum amount of maths in favour of geometrical reasoning.
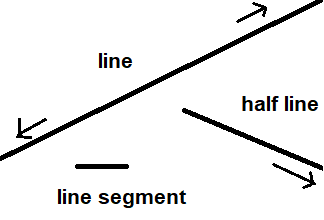
A line extends to infinity in both directions. It has no terminal point in accessible space.
A half line has a terminal point that we can access and its other end is 'at infinity'
A line segment has both ends accessible as terminal points.
In LOS determination we are dealing with line segments all the time but it is important to make sure that they are working as line segments and not as infinitely long lines!
A point on the 2D cartesian grid is denoted (x1,y1)
The terminal points of a line segment LS1 are ((x1,y1),(x2,y2))
If you want to retype all this HTML with subscripts - go ahead!
Two line segments - a long one - like a LOS/LOF LS1((x1,y1),(x2,y2))
A short one - the side of an obstacle or target etc. LS2((x3,y3),(x4,y4))
Return FALSE if the line segments don't intersect each other.
Return TRUE if the line segments intersect. If possible, recover the intersection coordinates.

Translate coordinates so that the origin is at the left end of the longer line segment.
Rotate the coordinates around this new origin so that the longer line segment lies along the positive x-axis
Use the new x coordinates of the shorter line segment to rule out one class of non-intersecting line segment pairs.
If the x coordinates of the shorter line segment are completely within the interval of the longer line then apply a simple test for intersection.
Calculate the actual intersection for the final class of difficult cases.
Select the longer line segment of the pair.
Line segment length is given by √((x1-x2)2+(y1-y2)2)
Retain the length of the longer line as longLineLength and ID the line it belongs to.
Working with the longest line segment identify the terminal point with the lowest x coordinate. Call it T1
Make T1 the coordinate origin for both line segments. That is perform a coordinate translation.
T1(x1,y1) ↠ T1t(0,0) origin shift is achieved by subtraction of (x1,y1) from all coordinate pairs.
T1t means T1 translated

Now rotate LS1t (LS1 translated) so that its other terminal point lies on the x-axis of the new coordinate system. This should be at coordinate (longLinelength, 0) after rotation through angle Θ
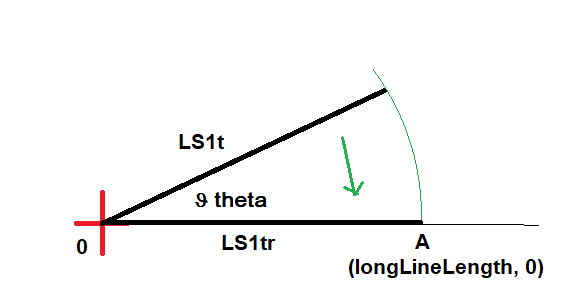
LS1tr line segment 1 translated and rotated can now be called OA.
Now rotate both terminal points of LS2t to obtain LS2tr or BC for short.
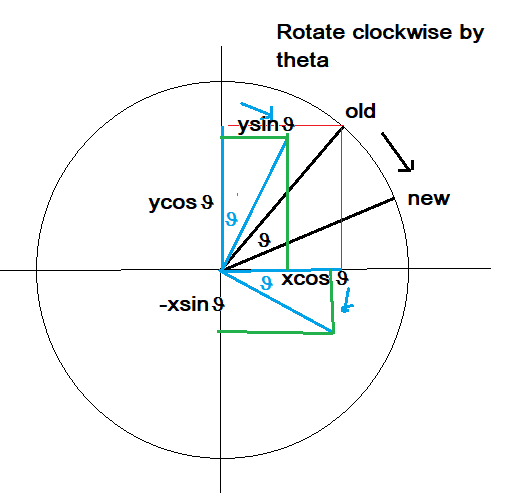
x → xcosΘ + ysinθ
y → -xsinθ +ycosθ
Working with the translated and rotated long line segment OA and the shorter line segment BC
there are 3 possible arrangements of the line segments in terms of BC's projection onto the x-axis.
In other words examine the x-coordinates of terminal points B avd C.
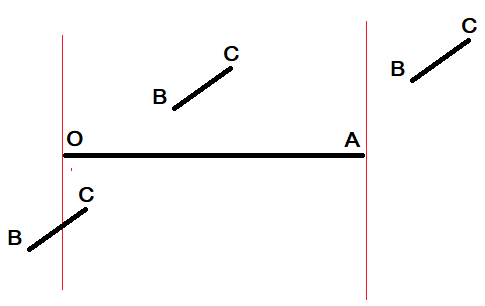
We can return FALSE for any BC line segments which have B and C x-coordinates that are both outside the interval OA.
Next consider BC line segments that are wholly within OA.
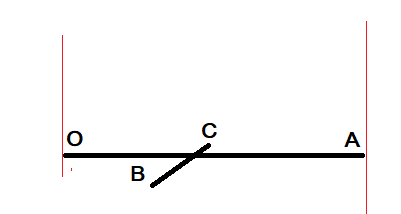
If BC has x-coordinates entirely within OA then it can only intersect OA if
BC's y-coordinates have opposite signs or one, or more, y-coordinates equals zero.
Test for this using yB*yC > 0 which is TRUE if BC doesn't touch or intersect OA
The final cases have one terminal of BC inside the interval, or at O or A, and the other terminal point outside the interval OA.
Intersection can only occur if the y Coordinates of B and C have opposite sign or one is 0 but the intersection can still miss OA. So do the y coordinate test first and then find the intersection if necessary.
To test for intersection in this case it is necessary to calculate the intersection point. This could also be done for TRUE results from within the interval as well.

In this case make B the left most (lowest x-coordinate) terminal of BC.
Gradient m of BC is given by m=(yC-yB)/(xC-xB)
Equation of BC in the form y=mx+c has c = yB-m*xB
Equation of BC is y = yB+m(x-xB)
Intercept with the x-axis given by setting y=0 occurs at x=xB-yB/m
For intersection this point must be in the interval OA
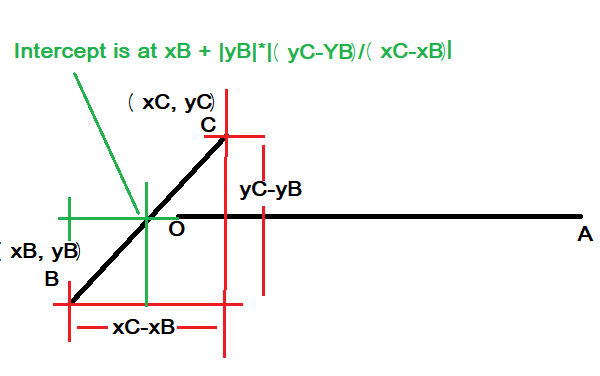
To recover the coordinates of the intercept in the original coordinate system it is necessary to reverse the rotation and then the translation. Use rotation by -theta and then add (x1,y1).