Pi Calculation
The aim of this session is to find a value of pi by taking the average of the perimeters of polygons drawn on the inside and outside of a circle.
You are going to edit a routine called "polyout. Once you have programmed this routine into Logo you can then call it just like one of the normal Logo commands.
Get Logo running in the normal fashion and then call up the routine editor by entering "polyout.
|
edit "polyout |  |
|
Now edit the code so that it reads like this. The easiest way to do this is to cut and paste it into the editor.
to polyout :sides :length sin and cos are examples of trignometric functions. These are essential tools for games programmers. | 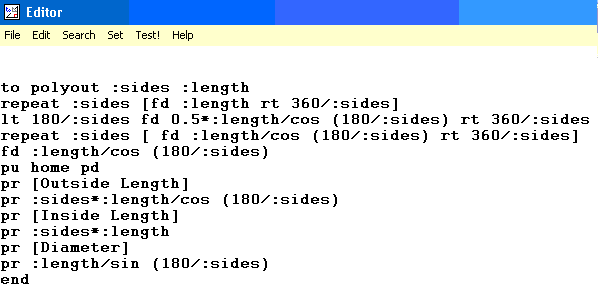 |
|
Now click on the "file" menu and select "save and exit". | 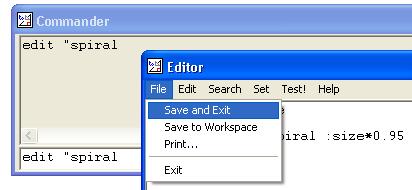 |
|
Now enter the command polyout 6 100 :size and :length are the arguments of the routine polyout. Polyout draws two n-agons which touch at the vertices of the inside one and the centre of the edges of the outer one. |  |
Tasks.
Make several different size polygon pairs. For each, use Excel to record the number of sides, inside length, outside length and diameter. Calculate the mean of the inside and outside perimeters. Then calculate a value for pi by dividing your mean value by the diameter
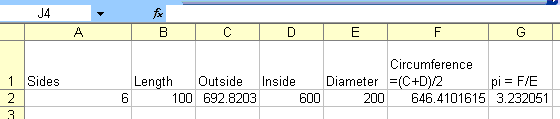
I used this formula in the circumference column
=(C2+D2)/2
and this one
=F2/E2
in the pi column.
Now make a Word document which fits onto one side of A4. This needs to contain a few images of polygon pairs, your data table, your final answer for the value of pi and reasons for deciding upon that value. How many dcimal places is your value accurate to?