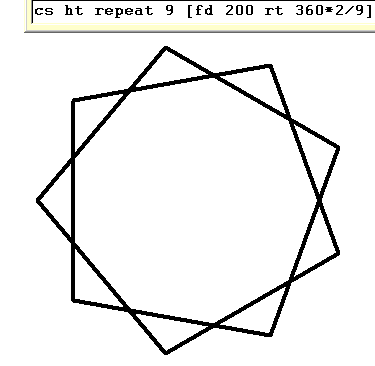
Pentagonal Star

Here is the code for a pentagonal star. Triangles and squares won't produce regular stellations(Why?).

cs ht repeat 5 [forward 120 right 360*2/5]

This works as follows:

1. cs ht clears the screen and hides the turtle.
2. repeat 5 makes the program do the stuff in side the brackets 5 times.
3. forward 120 draws a straight line 120 pixels long
4. right turns the turtle through the angle 360*2/5
5. 2 because you draw the first line of the stellation to the second vertex of the pentagon not the first.
6. 5 because you are working on a five sided polygon.

Drawing the Star

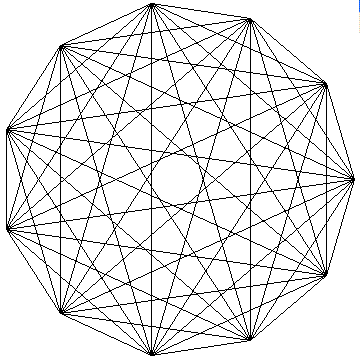
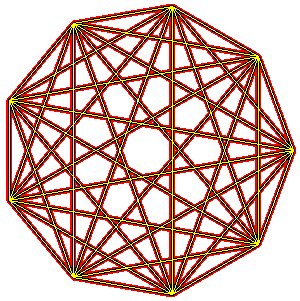
Heptagonal Stars

The heptagon has two distinct stellations.

Nine Points

cs ht repeat 9 [fd 200 rt 360*2/9]

Eleven Points

cs ht repeat 11 [fd 200 rt 360*5/11]

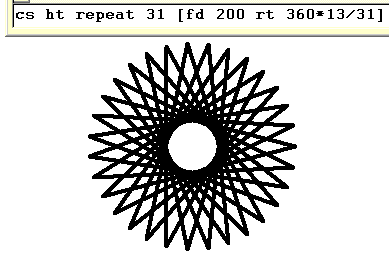
Thirty One Points

cs ht repeat 31 [fd 200 rt 360*13/31]

Tasks

Complete this table to show how many stellations there are for different polygons. Fill in the number of vertices and the start numbers which produce proper stellations. The first few rows have been done for you.

Questions

Why do some polygons allow stellations and not others?

Why do some polygons have more than one stellation?

Why are there some start numbers that don't work for a given polygon?

Which start numbers would produce stellations for a 19 sided polygon?

Harder Tasks

Write down the vertex order for the stellations of the heptagon. How does the start number relate to the number of orbits that you must make around the polygon before returning to the origin?

How could you use stellation to test for prime numbers?

What is the connection between the vertex number, the start number and their LCM (lowest common multiple)?

Fun Tasks

Use 'Print Screen' to drop your stellation into 'Paint' and then colour it in.

The program

Open Logo and the procedure editor. Copy and paste this code in and then save and exit.

to rose :verts
make "xpts (array :verts 0)
make "ypts (array :verts 0)
repeat :verts [
setitem repcount-1 :xpts first pos
setitem repcount-1 :ypts first butfirst pos
fd 100 rt 360/:verts ]
repeat :verts [
make "stpos repcount-1
repeat :verts [
pu setxy item :stpos :xpts item :stpos :ypts pd
make "cpos repcount-1
setxy item :cpos :xpts item :cpos :ypts pd]]
end

Call the procedure with the command line code:

rose 11

1. The make "xpts and "ypts commands record the position of the turtle at each vertex. The turtle then draws the outside polygon.
2. The program then works round each vertex in turn drawing a line to all the other vertices. This means that all the lines are actually drawn twice but the program runs so quickly that this isn't a problem.

In general terms the star polygons can be described using the notation (p/q) where p and q are positive integers which are usually co-prime. p is the number of vertices of the polygon and q is the vertex, counting from 0 to which the first line is drawn.
Thus for p = 7 the stellations possible are: (7/1) the heptagon, (7/2) and (7/3).

If p and q have a common factor then the stellation will not visit all the vertices. To overcome this the stellation can be rotated until all the vertices have been visited. This will result in patterns like the Star of David etc.

This exercise can also be thought of in terms of modular arithmetic. Stellation (10/3) requires three orbits to return to its origin (10mod3=1). Each orbit in effect performs a modular division.

Stellation (10/2) produces a pentagon as 10mod5=0. To produce a stellation from (10/2) it is necessary to draw the pattern once and then rotate to the unvisited vertices.