Tessellations. (Logo Version)
A tessellation is an arrangement of tiles fitting exactly together which can be extended as far as required in any direction.
Here are two tessellations:
|  |
The hexagons and the equilateral triangles have sides that are the same size. |
Task 1 Tiling the plane with regular polygons.
Your first mission is to find the three ways of completely tiling a flat surface (plane) using only one kind of regular polygon
Remember that regular polygons have equal sides and equal angles.
To do this you need to be able to draw a polygon
You should have done this before in previous Logo sessions. This is a reminder
Revision
This program draws an equilateral triangle.
repeat 3 [forward 40 right 120]
You can draw a square by using the code:
repeat 4 [forward 100 right 90]
The external angle of a polygon of n sides is 360/n
You can write a general polygon program as follows:
|
edit "poly | 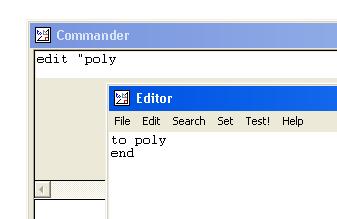 |
|
Now add the text that you can see in the picture. I've used the "set" menu to alter the font. to poly :length :sides |  |
|
Now click on the "file" menu and select "save and exit". | 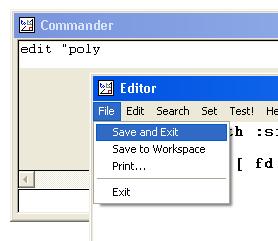 |
|
Now enter the command poly 60 6 This draws a hexagon with sides that are 60 pixels long. You can hide the turtle by typing ht. This stops it appearing in your designs. | 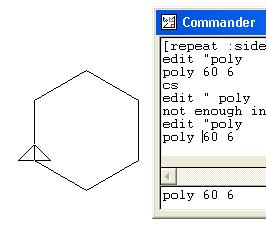 |
You can now draw one polygon but you need to draw several that meet at a common point or vertex.
To do this you are going to have to turn the turtle through the correct angle before drawing the next shape.
Here are a few attempts that are deliberately wrong.
Can you work out how to do it right?

|  |

|
|
It helps if you make another routine. This one draws a particular polygon and then moves the turtle to the correct position for drawing another polygon that is joined onto the first one. to pv :length :sides | 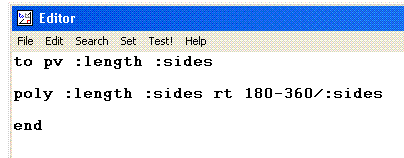 |
|
The pv routine has drawn an octagon and then turned through 135 degrees. It is now ready to draw something else. pv 80 8 | 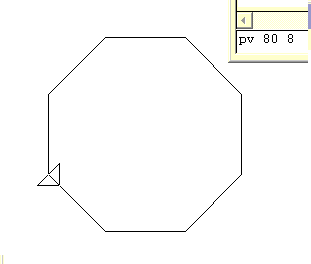 |
|
Thr routine has been called three times here. It has drawn an octagon, a duodecagon and a triangle. The problem is that they don't join up to make 360 degrees. pv 40 8 pv 40 12 pv 40 3 |  |
You should now know the three regular polygons which can be used, on their own, to tile the plane completely.
To demonstrate this in Logo you need to be able to draw the polygons around one vertex and then move the turtle to the next vertex.
|
4 squares around one vertex. repeat 4 [ poly 100 4 rt 90] |  |
|
You now need to move the turtle two full squares to the right and get it pointing upwards. repeat 4 [ poly 100 4 rt 90] rt 90 fd 200 lt 90 |  |
|
Then repeat the square drawing procedure. repeat 3[repeat 4[poly 50 4 rt 90] rt 90 fd 100 lt 90] For a better way to do this and to find out how to colour the square in go to Advanced Options at the bottom of the page. | 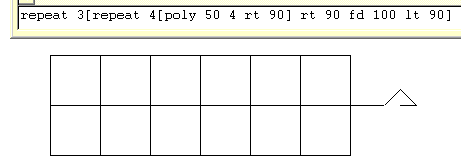 |
Task 1. Tile the Plane.
Apply what you have learned and tile the plane completely with patterns built up from one kind of regular polygon. Squares are easiest to use so do them first.
Have you worked out what the other two shapes are?
Can you get them to join together and produce a tiling?
Task 2. Tiling the Plane part 2.
|
You can also tile the plane by using combinations of regular polygons. There are 8 ways that you can do this. Each vertex must have the same number of the same type of polygon and the polygons must all have the same size side. |  |
|
To find the other 7 patterns first find sets of polygons that can be joined together around one vertex without overlapping or leaving gaps. There are actually 17 ways that you can fit polygons together around a vertex so that they total exactly 360 degrees. Only 7 of these can tile the plan without leaving gaps. (One vertex arrangement produces two distinct tilings. repeat 2 [poly 60 4 rt 90] poly 60 3 rt 60 poly 60 6 This code fits 2 squares, a triangle and a hexagon around one vertex. The problem is that you can't join this pattern up without leaving gaps. | 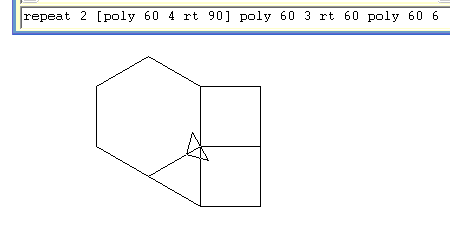 |
|
Here is a pattern that will tile the plane. Can you work out how to copy it so that it joins up without leaving gaps? poly 60 4 rt 90 poly 60 8 rt 135 poly 60 8 |  |
Advanced Options
|
Real programmers work by creating objects and then joining those objects together. You should only write a piece of code once. After that you just cut and paste or work with the object. We need to make squares and polygons with sides the same length. It also helps if we colour them in. edit "s Now enter this code. Remember to "save and exit" once you have put it in.
to s :size To run the code type: s 100 |  |
|
Now if we want to make 4 squares around one vertex all you need to type is: repeat 4 [ s 80 rt 90] |  |
|
A real programmer would now make this into an object called "sv". (square vertex). So type in edit "sv and enter this code.
to sv :sz You can then join whole blocks of squares together like this: repeat 4 [ sv 60 rt 90 fd 120] |  |
The task of finding the 17 vertex arrangements is quite challenging. This link takes you to an Excel spreadsheet which can be used to find angle combinations that add uo to 360 degrees. Save it to your my documents area before opening it. You can then run it in a separate window and look values up on it.
polygons.xls
|
Here's one to get you started! pv 40 4 pv 40 5 pv 40 20 It works because the angles of a square, pentagon and twentygon are 90, 108 and 162 degrees. These total to 360 degrees. This pattern will go all the way around the twentygon but it leaves gaps after that. | 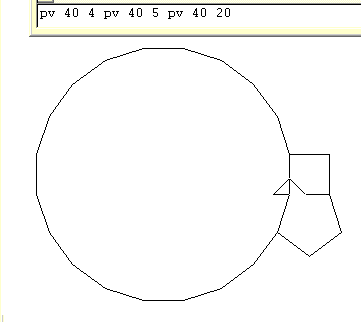 |