Working with Colour
To change the colour of the pen you need to use the setpencolor command.
setpencolor (list 0 0 255)
This will change the pen color to blue.
Computer languages like Logo tend to work in American and so use color not colour.
Computer colours are listed by three numbers which give their RGB values.
RGB is short for Red Green and Blue.
These numbers take values between 0 and 255.
For black use:
setpencolor (list 0 0 0)
For white (first turn the screen white and then use) use:
setpencolor (list 255 255 255)
 |
This program uses a for loop to generate a square which has a side equal to the counter on the repeat loop. The repeat loop counter also sets the color of the line used to draw the square. repeat 255 [setpencolor (list repcount repcount repcount) for [ x 0 4 1] [fd repcount rt 90]] |
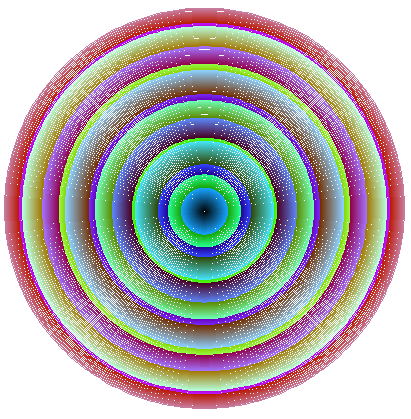 |
This program uses two routines, circle and colcircle, to draw a set of nested coloured circles. colcirc 200 200 |
|
to circle :rad :steps |
:rad is the radius of the circle |
|
to colcirc :rad :steps |
This program draws successive circles of increasing radii. The colours are set using the pencolor command acting on the remainders from dividing r by 3 different numbers. This program also uses a for loop. |
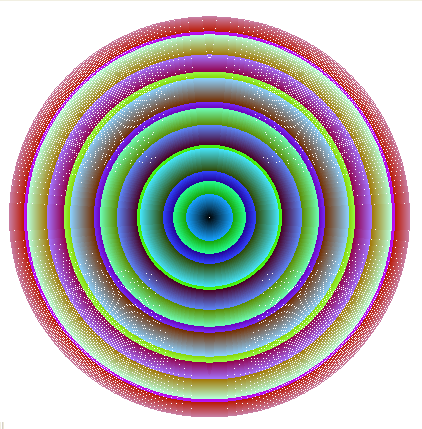 |
The pattern of white dots has a cause. Can you work out what is causing it? colcirc 200 1000 |
Filling Shapes with Colour
|
This code draws a square and fills it in. Remember to "save and exit" once you have put it in.
to s :size To run the code type: s 100 The colour works by moving the turtle inside the square, setting the fillcolour, filling in and then returning to the point that the turtle was at previously. |  |
Setting the Fill Color using an Index | |
|
This code also draws a square and fills it in. This time the code draws a square about the current turtle position. The code has two arguments; :size sets the edge of the square and :col 0-15 sets the fill color.
to s :size :col Test the code by typing s 200 2 etc. |
Turmite with core code; 
|
Reading the Color from the Pixel Beneath the Turtle | |
|
Reading a color from the screen is an essential skill for basic games. This code reads the color from the turtle position and uses this to decide what color to leave behind and which direction to move the turtle off in.
to main :size |
The pixel command returns the color value of the pixel at the turtle position.  Turmites are capable of extremely complex behaviour. This example locks into a steady pattern that expands outwards forever. The example above shows regions of very ordered behaviour and other regions of seeming chaos. The interaction of order and chaos makes these fascinating systems to study. |
Last updated 23rd February 2010