Complex Numbers

This page shows you how to use Logo with complex numbers. It enables you to plot functions in the complex plane with a colour representing a function of the complex coordinates.
Logo is not the ideal language for programming with complex numbers but it is a stepping stone towards Java etc. which would run the similar code but much more quickly. (Though getting graphical output is more complicated)

Creating a complex number

This requires the use of the list command. The real and imaginary components of the complex numbers are entered as the first and second elements of a list. This list can then be manipulated as an object in its own right.

make "z1 list 4 5
show :z1
[4 5]

This creates the complex number z1=4+5i and then "shows" it to you.

Modulus of a Complex Number

The modulus of a complex number z=x+iy is defined as:
|z|=SQRT(x²+y²)

To calculate this use the first command to extract the real component of z1 (from z1 which is received as the argument :l1 to the procedure cpmod) and first butfirst to extract the imaginary component. (butfirst decapitates the list.). The resulting modulus is returned as the output of the procedure.

to cpmod :l1
output sqrt ((first :l1)*(first :l1)+(first butfirst :l1)*(first butfirst :l1))
end

Call and test this procedure on a previously defined :z1 as follows:

make "z1 list 4 5
show cpmod :z1
6.40312423743285

Addition of Complex Numbers

The real and imaginary parts of a complex number are added separately to form a new complex number
z1=a+ib
z2=c+id
z1+z2=(a+c)+i(b+d)
To calculate this use the first command to extract the real components of z1 and z2. and first butfirst to extract the imaginary components. (butfirst decapitates the list.). A new complex number is created which is returned as the output of the procedure.

to cpadd :l1 :l2
output list (first :l1)+(first :l2) (first butfirst :l1)+(first butfirst :l2)
end

Call and test this procedure on previously defined :z1 and :z2 as follows:

make "z1 list 4 5
make "z2 list 2 -7
show cpadd :z1 :z2
[6 -2]

Multiplication of Complex Numbers

The multiplication of a complex numbers is defined as:
z1=a+ib
z2=c+id
z1*z2=ac-bd+i(ad+bc)

To calculate this use the first command to extract the real and imaginary parts of both numbers. The resulting product is returned as the output of the procedure.

to cpprod :l1 :l2
output list ((first :l1)*(first :l2)-(first butfirst :l1)*(first butfirst :l2)) ((first :l1)*(first butfirst :l2)+(first butfirst :l1)*(first :l2))
end

Call and test this procedure on a previously defined :z1 and :z2 as follows:

make "z1 list 4 5
make "z2 list 2 -7
show cpprod :z1 :z2
[43 -18]

Complex conjugate

The conjugate of a complex number is its image in the line y=0. It is very useful in the division of complex numbers. It is formed by reversing the sign of the imaginary part of z
z1=a+ib
z1 conjugate=a-ib
To calculate this use the first command to extract the real component of z1. and first butfirst to extract the imaginary component. (butfirst decapitates the list.). A new complex number is created which is returned as the output of the procedure.

to cpcon :l1
output list (first :l1) -1*(first butfirst :l1)
end

Call and test this procedure on previously defined :z1 as follows:

make "z1 list 4 5
show cpcon :z1
[4 -5]

Reciprocal of a complex number

The reciprocal of a complex number is defined as:
z1=a+ib
z1r=a-ib/(a²+b²)
z1*z1r=1
In other words it is the conjugate of the number divided by the square of the modulus.

To calculate this use the first command to extract the real and imaginary parts of both numbers. The resulting product is returned as the output of the procedure.

to cprecip :l1
localmake "modsq ((first :l1)*(first :l1)+(first butfirst :l1)*(first butfirst :l1))
output list (first :l1)/:modsq -1*(first butfirst :l1)/:modsq
end

Call and test this procedure on a previously defined :z1 and :z2 as follows:

make "z1 list 4 5
show cprecip :z1
[0.0975609756097561 -0.121951219512195]

Subtraction of Complex Numbers

The real and imaginary parts of a complex number are subtracted separately to form a new complex number
z1=a+ib
z2=c+id
z1-z2=(a-c)+i(b-d)
To calculate this use the first command to extract the real components of z1 and z2. and first butfirst to extract the imaginary components. (butfirst decapitates the list.). A new complex number is created which is returned as the output of the procedure.

to cpsub :l1 :l2
output list (first :l1)-(first :l2) (first butfirst :l1)-(first butfirst :l2)
end

Call and test this procedure on previously defined :z1 and :z2 as follows:

make "z1 list 4 5
make "z2 list 2 -7
show cpsub :z1 :z2
[2 -2]

Division of Complex Numbers

The division of two complex numbers is defined as:
z1=a+ib
z2=c+id
z1/z2=((ac+bd)+i(bc-ad))/|z2|²

z1/z2=z1*(conj)z2

To calculate this use the first command to extract the real and imaginary parts of both numbers. The resulting product is returned as the output of the procedure.

to cpprod :l1 :l2
localmake "modsq ((first :l2)*(first :l2)+(first butfirst :l2)*(first butfirst :l2))
output list ((first :l1)*(first :l2)+(first butfirst :l1)*(first butfirst :l2))/:modsq ((first :l2)*(first butfirst :l1)-(first butfirst :l2)*(first :l1))/:modsq
end

Call and test this procedure on a previously defined :z1 and :z2 as follows:

make "z1 list 4 5
make "z2 list 2 -7
show cpdiv :z1 :z2
[-0.509433962264151 0.716981132075472]

This program draws a basic version of the Mandelbrot set. Java is much quicker (well nigh essential if you want to really study this kind of fractal) but there is an arcane satisfaction to be had from getting good old Logo to do it! The procedure uses cpadd, cpprod and cpmod. A pair of nested loops track through the x and y coordinates. A modular division function is used to generate colour contours.

to mbrot :iter :x0 :y0
penpaint
for [x (:x0-1.5) (:x0+1.5) 0.01] [
for [y (:y0-1.5) (:y0+1.5) 0.01] [
make "z0 list :x :y
make "c0 list :x :y
pu home fd :y*100 rt 90 fd :x*100 pd
make "count 0
while [and ((cpmod :z0 )<4) (:count < :iter)] [
make "z0 cpadd (cpprod :z0 :z0) :c0
make "mod cpmod :z0
make "count :count+1
]
make "red (remainder :count 3) *80
make "green (remainder :count 5)*50
make "blue (remainder :count 4)*60
setpencolor (list :red :green :blue) fd 1
]]
end

Call the procedure using:

cs ht mbrot 10 -0.5 0

The arguments sent to the procedure are the depth of iterations used (higher gives more detail but less speed) and the coordinates of teh centre of the plot.
This program could be refined to allow you to zoom in on areas of interest!

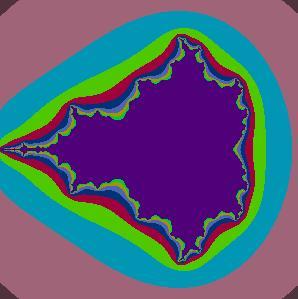
The Mandelbrot set is a mapping of the complex plane. The x coordinate represents the real part of the complex number z=x+yi and the y coordinate represents the imaginary part.

i is the square root of -1.

The mapping used is z - z²+c where z and c are both complex numbers. This mapping either heads for a fixed value of magnitude less than 2 or grows to infinite size. The colours on the image indicate how big the iterated number z gets.

To generate the Mandelbrot set z is initially set to 0 and c is of the form x+yi giving the (x,y) coordinates of a point on the complex plane. The program then maps z as z²+c and colours the initial c value accordingly.

When z is squared the following results for z=a+bi
z²=a²+2abi-b² (as i²=-1)
This has a real part equal to a²-b²
and an imaginary part equal to 2abi
The start value of c is added to this and the process repeats. In other words the mapping can also be thought of as
x goes to a²-b²+x
y goes to 2ab+y
Where (x,y) is the starting value of c and provides the initial values of a & b respectively.

Last updated 16th November 2009