Cycloids of Revolution (Spirograph patterns.)

If you roll a circle along a straight line then the curve generated by a point on the circle's circumference is known as a cycloid.

If you roll a circle (c1) along a the outside of another circle then the curve generated by a point on the circumference of c1 is known as an epicycloid.

If you roll a circle (c1) along the inside of another circle then the curve generated by a point on the circle's circumference is known as a hypocycloid.

Cycloids and their related curves are much easier to execute in GeoGebra than in Logo or Excel. All you need is the maths below and the parametric curve command.

Curve[x-expression, y-expression, parameter,parameter start, parameter finish]

Curve[(a + b)*cos(wa*t) + b*cos(wb*t), (a + b) sin(wa*t) + b*sin(wb*t), t, -100, 100]

Curve[(a + b)*cos(wa t) + (b + c)*cos(wb*t) + c*cos(wc*t), (a + b)*sin(wa*t) + (b + c)*sin(wb*t) + c*sin(wc*t), t, -100, 100]

Use sliders to control the parameters a,b and c in the equations.

The GeoGebra worksheets for these can be downloded here: Cycloids, Megacycloids.

Cycloid

Epicycloid

Hypocycloid


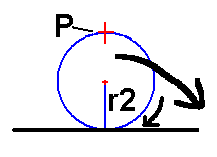This is the basic image to use when trying to understand the other two curves.
All you do is cut the circle that is being rolled around, straighten it out to a line and study how the circle rolls along it. Then bend the line back into a circle.

In the epicycloid the rolling circle rolls clockwise and rotates clockwise.
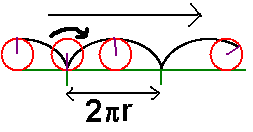
In a hypoycloid the rolling circle rolls clockwise but rotates anticlockwise!

Theory

Imagine that our circles are start on top of each other and then the smaller one rolls clockwise around the larger one.
After a while the pen (which doesn't actually have to be on the rim of the circle) will be in the position shown as P.
The circles have both rolled through an arc length t but the smaller circle will have turned through a larger angle.
Thus the direction of the radius that points to P is no longer in the same direction as that of the radius to the point where the circles touch.
Note that angle B is measured with respect to the line joining the centres of the two circles. B is given by 360t/2PIr2 but the frame of reference that it is drawn against has rotated by angle A.

We need a program that does a few straightforward things:

  1. Finds the angle A that the bigger circles radius, r3, has turned through.
  2. Rotates the turtle through A and then moves the turtle distance r3+r2 to the centre of the moving circle.
  3. Rotates through B so that the turtle is pointing towards P.
  4. Moves through distance r1 and draws a point at P.
  5. Repeats this process sufficient times to draw the full curve.

This program draws epicycloids and hypocycloids.

to cyc2 :r1 :r2 :r3 :plots
make "t 0
repeat :plots [
pu home
rt :t*360/(2*PI*:r3)
fd :r2+:r3
rt :t*360/(2*PI*:r2)
fd :r1-1 pd fd 1
make "t :t+0.1 ]
end

2*PI*r calculates the circumference of a circle. t the distance moved by the circle divided by circumference gives the fraction of the a full 360 degree rotation that the circle must turn through to do this.
Plots is simply how many times the repeat loop repeats. Each repeat adds another dot to the drawing.
t is a parameter that represents distance rolled or time elapsed. You can alter the value of 0.1 which increments t on every cycle through the repeat loop.

Save and exit then type this command to test your code:

cyc2 50 50 50 2500


You should get this shape. Read the notes with the introductory (and other) diagrams to understand why.

Remember
r1 is the distance from the centre of the rolling circle to the "pen's" position
r2 is the radius of the rolling circle
r3 is the radius of the circle that you are rolling around.

Further tests.


The rolling circle has half the radius of the stationary one.

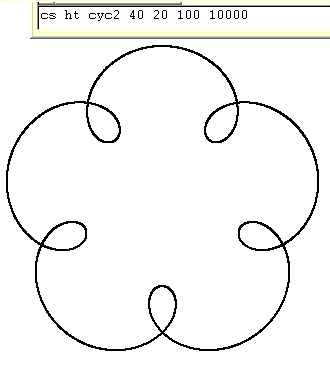The rolling circle has one fifth the radius of the stationary one.
The drawing point p's radius r1 is twice the radius of the rolling circle r2 (impossible in spirograph!).
The rolling circle makes 5 rotations for one orbit of the stationary circle.
Because r1 is greater than r2 "epicyclic" loops are generated.

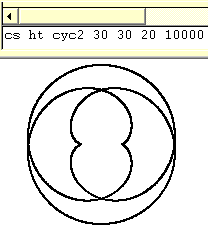The rolling circle has a radius 3/2 times greater than the stationary one.
The rolling circle makes 2/3 of a rotation for one orbit of the stationary circle.
The pattern takes 3 orbits to reach completion.

Further challenges.


The radius of the rolling circle is a factor of that of the stationary circle. Use this to predict how many loops or orbits you need to obtain a closed loop.

What happens if r2 is not a factor of r3?

This is the hypocycloid version of the previous curve. You can generate hypocycloids with your existing program.
Think about the information in the introductory drawings. It is a very easy thing to do once it clicks!

How can you draw a hypocycloid?

It is quite easy to modify your program to generate cycloids. Try to do this too.

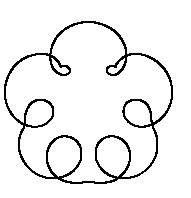This is what happens if the stationary circle in your version of the program is made to rotate around another circle!

Modify your program to allow the stationary circle to roll as well.
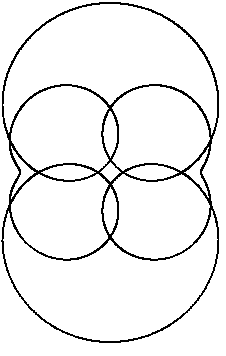