Line Fractals
LOGO is particularly suited to the production of line fractals. Fractals are continuous line drawings which have the property of looking similar at any viewing scale. If you magnify a fractal then it just looks the same. They have an infinite level of detail
Midpoint Displacement Fractals.

|
How to draw an example.
|
Drawing MPTD Fractals with Logo.Open LOGO and the procedure editor. Copy and paste this code in and then save and exit.
to mptfrac :x1 :y1 :x2 :y2 :level Call the procedure with the command line code: mptfrac -150 0 150 0 5 |
|

|
This type of fractal is often used to generate virtual landscapes for computer games. |

| |
Levy Fractal
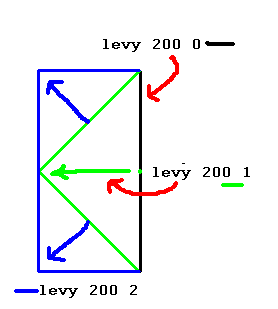
|
The Levy fractal is an example of a midpoint displacement fractal. |
|
This program draws the Levy fractal.
to levy :size :level Test the program by typing | 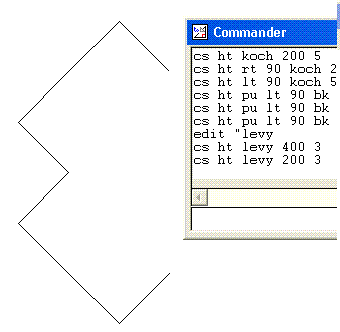 The program works by using a very important idea called recursion. The program checks to see if at has reached level 0. If it hasn't then it calls itself, again, but tells itself to make several more, smaller copies. Make sure that you reduce the level by 1 on each recursive call. (What happens if you don't?) |
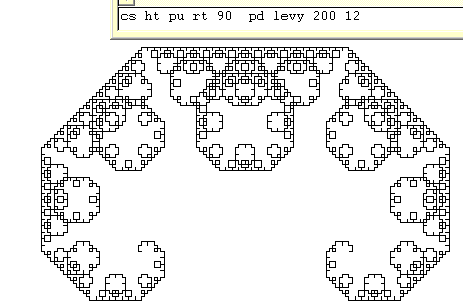
|
This is the same curve but at much deeper level of recursion. |
Koch Fractal
|
This is an example of a fractal that is generated by taking each line segment of the existing curve and replacing it with a specific set of line segments. |
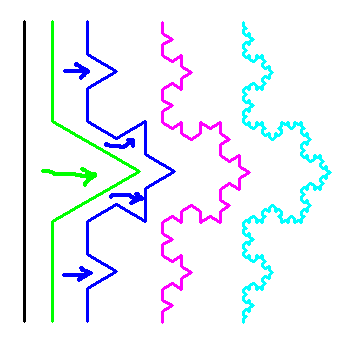
|
|
This is the code for the Koch fractal.
to koch :size :level You can test this program by typing |
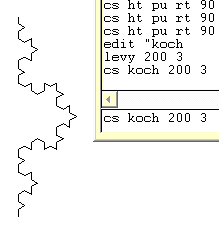
|
Other Line Fractals
|
Here are several variations on this theme. All are constructed from similar commands. The main things to do are to think about the angles that you want your curve to turn through and how much it needs to shrink at each iteration. This amount of shrinkage is linked to the concept of "fractal dimension". These fractals have a fractal dimension lying between 1, a straight line, and 2, which is a flat area of the plane. | |

|
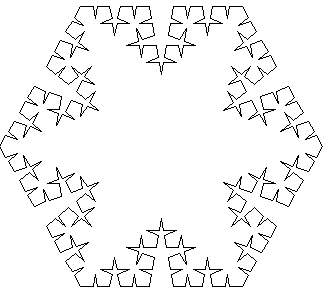
|

|
|

| |
Last modified 25th January 2010