Turmites
Turmites are miniature computers. They read the colour of the square that they are sat on. They then set the colour of that square before moving in a particular direction. Though this instruction set is very small turmites are capable of very complex calculations. There is no short cut to calculating what a particular turmite will do. The quickest way to find out what it does is to run it and see. This concept lies at the core of Turing's halting problem and his version of Godel's incompleteness theorem.
Use the code below to first make program s. You need s to colour in the squares under the turmite.
Then make program main. This creates a turmite.
To make further turmites it is probably best to copy your first main section and rename it main2 etc.
Then alter the central block of if statements to produce new turmites.
Setting the Fill Color using an Index | |
|
This codedraws a square and fills it in. The code draws a square about the current turtle position. The code has two arguments; :size sets the edge of the square and :col 0-15 sets the fill color.
to s :size :col Test the code by typing s 200 2 etc. If this doesn't work at first try cs to clear the screen. |
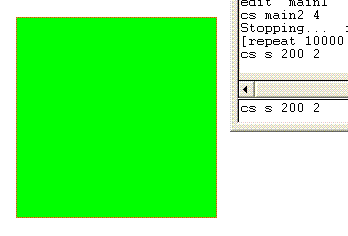
|
Reading the Color from the Pixel Beneath the Turtle | |
|
Reading a color from the screen is an essential skill for basic games. This code reads the color from the turtle position and uses this to decide what color to leave behind and which direction to move the turtle off in.
to main :size |
The pixel command returns the color value of the pixel at the turtle position.  Turmites are capable of extremely complex behaviour. This example locks into a steady pattern that expands outwards forever. The example above shows regions of very ordered behaviour and other regions of seeming chaos. The interaction of order and chaos makes these fascinating systems to study. |
|
Turmite with core code; 
This turmite produces a pattern with both chaotic and ordered elements. It seems to be infinite in that it gradually expands to fill the plane. Does it ever stop? |
Turmite with core code; 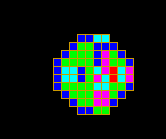
There are an infinite number of turmites to play with. Their behaviour boils down to 4 main classes. Can you find all four? |
Last updated 3rd February 2012