Square and Triangle Fractal
This uses two procedures s and t which call each other recursively. That is each calls itself as part of its own definition. This is a very powerful programming idea but it has to be used carefully as it is a very effective way to either run out of memory or lock your computer up.
s
This procedure constructs a square on the line (x1,y1) (x2,y2) passed to it in the procedure call.
If the level is 0 then the program stops. Always make sure that a recursive procedure has a stop call and that the procedure runs towards and not away from it!
to s :x1 :y1 :x2 :y2 :level
ifelse :level=0 [stop][
local "x3
local "x4
local "y3
local "y4
make "x3 :x1-(:y2-:y1)
make "y3 :y1+(:x2-:x1)
make "x4 :x2-(:y2-:y1)
make "y4 :y2+(:x2-:x1)
pu setxy :x1 :y1 pd
setxy :x3 :y3
setxy :x4 :y4
setxy :x2 :y2
setxy :x1 :y1
pu setxy (:x1+:x4)/2 (:y1+:y4)/2 pd
setfc 3 fill
t :x3 :y3 :x4 :y4 :level-1
]
end
|

The variables are made local so that they don't interfere with subsequent calls to the procedure.
The other vertices of the square are found by using the fact that a square can be generated on any line by rotating the line through ninety degrees. This is equivalent to subtracting (y2-y1) from x1 and adding (x2-x1) to y1.
The square is then drawn and coloured in.
Finally t is called with level reduced by one. t is placed on the top edge of the square.
x3=x1-B
y3=y1+A
x4=x2-B
y4=y2+A

|
t
This draws an isocoles triangle on any line supplied with a height equal to half the length of the base line.
to t :x1 :y1 :x2 :y2 :level
ifelse :level=0 [stop][
local "x3
local "y3
local "l
make "l sqrt ((:x2-:x1)*(:x2-:x1)+(:y2-:y1)*(:y2-:y1))
make "x3 :x1-0.5*(:y2-:y1)+0.5*(:x2-:x1)
make "y3 :y1+0.5*(:x2-:x1)+0.5*(:y2-:y1)
pu setxy :x1 :y1 pd
setxy :x3 :y3
setxy :x2 :y2
setxy :x1 :y1
pu setxy :x1-0.25*(:y2-:y1)+0.5*(:x2-:x1) :y1+0.25*(:x2-:x1)+0.5*(:y2-:y1)
pd
setfc 3 fill
s :x1 :y1 :x3 :y3 :level-1
s :x3 :y3 :x2 :y2 :level-1
]
end
|
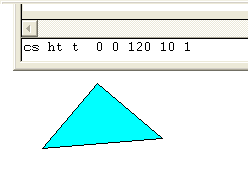

|
Square and Triangle

|
Square Starfish

|
Tree Forgery

|
|
|
|






