Working with Numbers Part 1

Basics Repeating Problems 1 Procedures Problems 2 Remainders Problems 3

Basic Operations

Using Logo to perform multiplication, addition, division and subtraction is very similar to doing it in Excel or on a programmable calculator.
Type the problem into the command line and press return to get the answer. Spaces between parts of the problem don't matter but you can use brackets to simplify expressions.

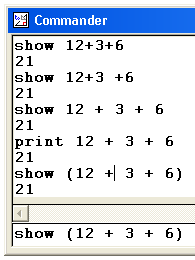
Addition

show 12 + 3 + 6

show 12 + 3 + 6

print 12 + 3 + 6

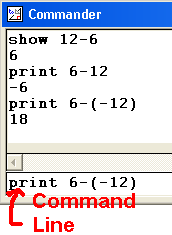
Subtraction

show 12-6

print 6-12

print 6-(-12 )

Multiplication

show 12*6

print 6*12

print 6*(-12 )

print 6*-12

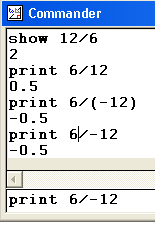
Division

show 12/6

print 6/12

print 6/(-12 )

print 6/-12

To make the output look better you can modify the print statement like this:

(print "The "answer "to "4 "times "165789 "is 4*165789 )

To get an ordinary word to print as a word you must put a " in front of it.
4*165789 doesn't have a " so the computer calculates it.

Using make, repeat and repcount.

Make

Make is a very useful command. It enables you to tell the computer to give a particular variable a given value.
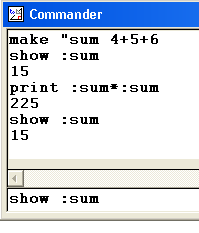
For instance you might call a variable sum and then tell the computer the sum to do.

make "sum 4+5+6
show :sum
print :sum*:sum

You must put a " in front of a variable when you are changing its value and : in front of it when you use it in a formula.

Repeat

Repeat tells the computer to do a certain job several times.

make "sum 0 repeat 4 [show :sum make "sum :sum + 10 ] show :sum

Repeat statements need [ square brackets ]. You need to make sure that :sum is set to 0 at the start of this program.


make "product 1 repeat 8 [show :product make "product :product *5 ] show :product

You need to make sure that :product is set to 1 at the start of this program.


Repcount

repcount tells the computer how many times a repeat loop has been done.

repeat 5 [show repcount]
make "sum 0
repeat 5 [make "sum :sum + repcount show :sum]

Repeat statements need [ square brackets ].
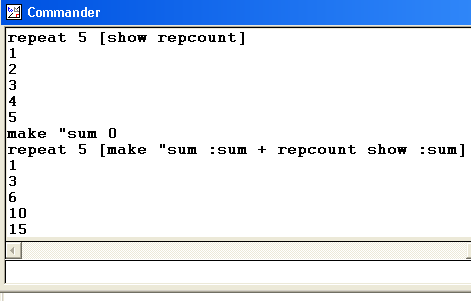You need to make sure that :sum is set to 0 at the start of this program.

You can combine commands onto oneline, as shown below; this makes it easier to understand what is happenning.

Problems 1

  1. Use Logo to find the nth triangular number.
  2. Use Logo to find the nth power of a number.

Start a Word document to record your solutions and answers to these problems. You can cut and paste into and out of Logo.

Triangular numbers

Triangular numbers can be found by adding the whole numbers together, in order, starting from 1. Thus:
T1=1
T2=1+2=3
T3=1+2+3=6
T4=1+2+3+4=10

Use Logo to find T5, T10 and T100

Powers

The nth power of a number is that number multiplied by itself n times.
62=6*6=36
43=4*4*4=64
84=8*8*8*8=4096

Use Logo to find 255, 225 and 12344

Writing Procedures.

A procedure is a set of several lines of instructions which the computer remembers and which you can call upon to do something.

We will write a procedure to calculate cubes.
You have already found cubes by typing them directly into the command line eg:

show 4*4*4

Procedures save time and effort in the long run and can do much more complicated things than single lines entered at the command line.

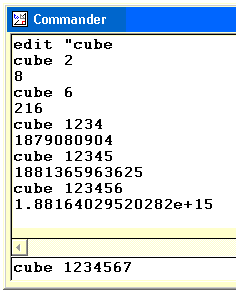
Calling up the Editor

The procedure editor is called by typing:

edit "cube

The editor screen will appear. Type this code in. It is a simple procedure which finds and prints the cube of a variable called :number which you send to the procedure when you call it.

to cube :number
print :number*:number*:number
end

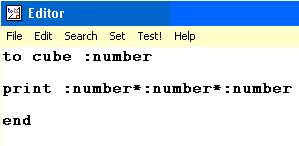Saving your procedure.

Now select file and save and exit. This will save your program to RAM. You must also use save in the main Logo screen if you want to save your program to disc.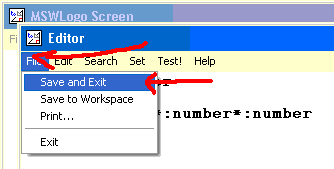


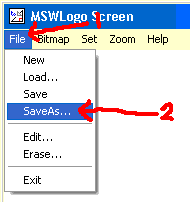Testing procedures.

Now test your procedure by calling it to calculate some cubes. Start with ones that you know:

cube 2
cube 6
cube 1234
cube 1234
cube 12345
cube 123456

The first 5 answers are exact. Logo has given an integer (whole number) answer. The final answer is too big for Logo to cope with in integer format and so it has switched to standard form. This answer is no longer exact. If you want to find the exact value of a big cube then use must write a special procedure or use a program like derive

Problems 2

  1. Write a procedure to find the sums of the squares of two numbers.
  2. Write a procedure to find the sums of the cubes of two numbers.

Start a Word document to record your solutions and answers to these problems. You can cut and paste into and out of Logo.

Sums of squares

Write a procedure to find the sums of the squares of two numbers.

For example:
32+42=3*3+4*4=25

Here is the print out from my solution. It shows the sums of squares of the numbers 1&1 2&1 2&2 etc. up to 3.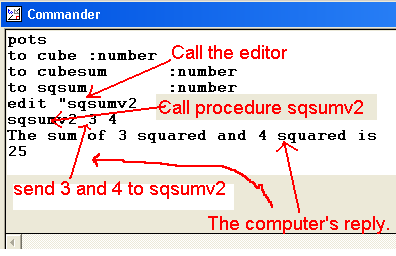

Here is a different solution which works on two numbers at a time. You tell the machine which numbers to work with.

Sums of cubes

Write a procedure to find the sums of the cubes of two numbers.

For example:
33+43=3*3*3+4*4*4=91

Here is the print out from my solution. It shows the sums of cubes of the numbers 1&1 2&1 2&2 etc. up to 3.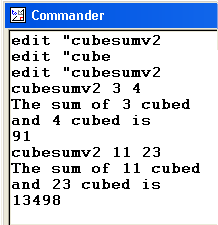

Here is a different solution to the same problem.

Remainder, if and ifelse.

Remainder, if and ifelse are three useful commands which allow you to write a large number of useful programs.

remainder

This outputs the remainder of the first number divided by the second number.

For example:

print remainder 10 6
print remainder 6 10
print remainder 100 10
print remainder 55 10.2

Remainder only works with integers (whole numbers.)

if

This executes a piece of code only if a certain condition is true.

For example:

if (6*8=48) [print "true]
if (6*8=59) [print "false]
repeat 9 [if ((remainder repcount 2) = 0) [print repcount]]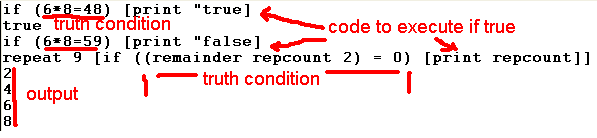

The first command printed true as 6*8 is indeed 48.
The second command gave no output as 6*8 isn't 59.
The third command prints the value of repcount in the repeated bracket if repcount is even, that is, if it leaves remainder 0 on division by 2.

ifelse

This executes one piece of code if a certain condition is true and does something else if it isn't.

For example:

ifelse (6*8=48) [print "true] [print "false]
ifelse (6*8=59) [print "true][print "false]
repeat 9 [ifelse ((remainder repcount 2) = 0) [(print repcount "is "even)][(print repcount "is "odd)] ]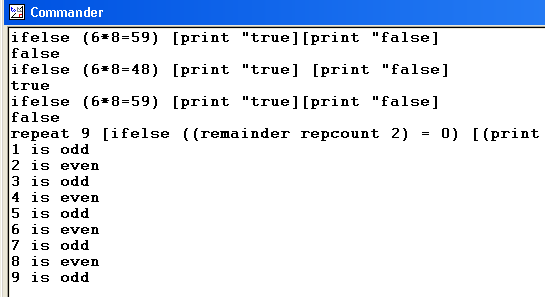

The first command printed true as 6*8 is indeed 48.
The second command printed false as 6*8 isn't 59.
The third command printed odd if repcount gave remainder 1 on division by 2 and even if repcount gave remainder 0 on division by 2.

Problems 3

  1. Write a procedure to find the factors of a number.
  2. Write a procedure to find the prime factors of a number.
  3. Write a procedure to find the highest common factor, HCF, of two numbers.
  4. Write a procedure to find Pythagorean triples. (3,4 and 5 or 5, 12 and 13 are such numbers)

Start a Word document to record your solutions and answers to these problems. You can cut and paste into and out of Logo.

Factors

Write a procedure to find the factors of a given number.

For example:
The factors of 12 are 1,2,3,4,6,and 12.
The factors of 19 are 1,and 19 because 19 is prime.

Here is the print out from my solution. It shows the factors of 24.
There are lots of ways to do this but some methods are much more efficient than others. In computer speak efficient means fast and requiring the minimum of code, memory or processor time.

Prime factors.

Write a procedure to find the prime factors of a given number.

For example:
The prime factors of 12 are 2,2,and 3.
2*2*3 = 12

The prime factors of 51 are 3 and 17.
3*17 = 51

Here is the print out from my solution. It shows the prime factors of 144 and 191.

Final Challenge

What is the relationship between the pairs of numbers situated opposite each other in the diagram below?

Fill in the other boxes. You are only allowed numbers below 100 and you can only have each number once.

All the programming tricks that you need have been demonstrated on this webpage.

last modified 4th February 2012