Working with 2D Graphics

Working with Basic 2D Graphics.

You should have had a very good look at all the basic Logo exercises on the "Getting Started with Logo" pages. In particular you should be happy with editing and saving procedures and all aspects of drawing polygons.

Drawing an object
The easiest way to do 2D graphics is to use Logo's built in commands for translation and rotation etc. Suppose you want to draw an object called object. Write a procedure called object to draw the object. to object repeat 4 [ repeat 3 [fd 50 rt 120] rt 90 ] end
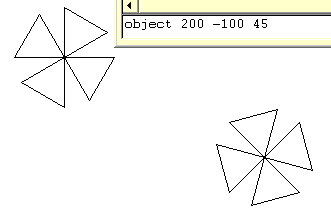
Now suppose that you want to draw this object at coordinates (x,y) and at an angle A to the vertical. You could modify object to look like this: to object :xCo :yCo :angle pu home setxy :xCo :yCo rt :angle pd repeat 4 [ repeat 3 [fd 50 rt 120] rt 90 ] end This enables you to draw an object of your choosing, anywhere on the screen at any angle that you like. The problem comes if you want to draw bigger and smaller copies of the object or you want to distort it in some way. (to simulate perspective effects etc.)
One solution to this problem, which also lays the foundation for a more advanced way of drawing objects is to always make object at one size but then magnify it by a scale factor. to object :xCo :yCo :angle :scaleFactor local "size make "size 10*:scaleFactor pu home setxy :xCo :yCo rt :angle pd repeat 4 [ repeat 3 [fd :size rt 120] rt 90 ] end "size is an example of a local variable. It is local to this instance of object and is not passed to any other procedures. This is useful as it prevents procedures messing each other up.

Working with 2D Vector Graphics.

3D graphics is possible in two ways within Logo. This section will look at 2D graphics in a way that makes the better way of doing 3D graphics more accessible.

The aim is again to draw a an object which is made from a collection of points (vertices) joined by lines (edges). We will write several procedures to enable us to draw this object anywhere, at any angle, to any scale and distorted in various ways.

Object Drawing with Vectors

Think of the object as a collection of points which are joined by lines.
To make life easier, start with one vertex on the origin (0,0).
This can be turned into Logo as follows:

to object2
setxy 0 0
setxy 10 0
setxy 10 10
setxy 5 20
setxy 0 10
setxy 0 0
end

A better way to do this is to turn the points into a list of coordinate pairs.
These can be entered in the command line as follows:

make "a list 0 0
make "b list 10 0
make "c list 10 10
make "d list 5 20
make "e list 0 10
make "obj2 (list :a :b :c :d :e :a)

We now need a program which can convert a coordinate list (of any length) into a drawing.

to draw :object
setpos first :object
make "object butfirst :object
ifelse (count :object)=0 [stop][ draw :object]
end

This program takes the list which it calls object as its argument. It then moves the mouse to the first pair of coordinates in the list.
The butfirst command then chops the first pair of the list.
If the list has length 0 then the procedure stops.
If there are still coordinate pairs left in the list then the procedure calls itself to carry on the drawing.
A procedure which invokes itself is recursive. You mus make sure that it is able to stop at some point!

To draw the object call draw at the command line with:

draw :obj2

Translation

Now we want to draw the object at any point (x,y) on the screen.
To do this we need a procedure that will translate our object by the amount (x,y).

to trans :object :xCo :yCo
localmake "point (array 2 1)
localmake "points (array count :object 1)
repeat count :object [
setitem 1 :point (first item repcount :object)+:xCo
setitem 2 :point (last item repcount :object)+:yCo
setitem repcount :points ( arraytolist :point)
]
output arraytolist :points
end

First two local arrays are made to hold the pairs of coordinate points.
These are then translated by the amounts xCo and yCo.
Then the coordinates are output as a list of coordinate pairs.
The procedure can cope with a list of coordinate pairs of any size.

To test this procedure we need to write a modifier to draw. This is because draw currently assumes that it is already in the correct place to begin drawing. The modified procedure is shown below.

to drawpos :object
pu setpos first :object pd
draw :object
end

This simply moves the turtle position to the first coordinate pair in the list and then tells the program to get on and draw.

Test the code with a command line call something like this:

cs repeat 5 [drawpos trans :obj2 repcount*10 repcount*20]

Enlargement

The code for enlarging an object is very similar to that for translating it. The difference is that the coordinate pairs are multiplied by a scale factor rather than having a translation vector added.

to scale :object :xSc :ySc
localmake "point (array 2 1)
localmake "points (array count :object 1)
repeat count :object [
setitem 1 :point (first item repcount :object)*:xSc
setitem 2 :point (last item repcount :object)*:ySc
setitem repcount :points ( arraytolist :point)
]
output arraytolist :points
end

Test with this command line statement:

cs repeat 5 [drawpos scale :obj2 repcount*4 repcount*1.5]

(	x'	)	=	(	xSc	0	)	(	x	)
	y'				0	ySc			y

An enlargement written in matrix notation.

Rotation

Rotation is harder to accomplish but the struggle is worth it because it paves the way for working in 3D.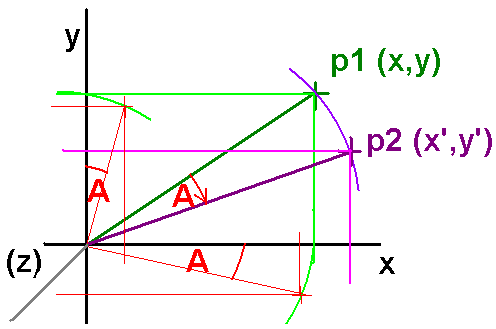
First a bit of trigonometry. Consider the effects of rotating a point (x,y) by an angle A.

Think about what happens to the x and y components of the vector joining p1 to the origin.
These are both rotated by the same angle A that p1 is rotated by.

Thus our new x coordinate x' is given by

x'= xcosA + ysinA

Whilst the y' coordinate is given by:

y'= -xsinA + ycosA

For reasons that will become obvious when we hit 3D this is more easily represented as a matrix multiplication of the position vector (x, y)

(	x'	)	=	(	CosA SinA	)	(	x	)
	y'				-SinA CosA			y

This is the standard matrix notation for a clockwise rotation A about the z axis which sticks out towards the viewer looking down on the xy plane.

So to turn this idea into a usable Logo procedure all we need is a procedure that will apply a general rotation A to our (x,y) coordinate pairs.

to rotz :object :A
local "newX
local "newY
localmake "point (array 2 1)
localmake "points (array count :object 1)
repeat count :object [
make "newX ((first item repcount :object)*cos :A)+((last item repcount :object)*sin :A)
make "newY (-(first item repcount :object)*sin :A)+((last item repcount :object)*cos :A)
setitem 1 :point :newX
setitem 2 :point :newY
setitem repcount :points ( arraytolist :point)
]
output arraytolist :points
end

Test this code with our object :obj2 and this command line instruction:

cs draw rotz :obj2 45

It is always worth giving your code a good testing. This is a procedure which invokes all three of our operations in sequence. It draws a randomly scaled and rotated version of obj2 at a random point on the screen. The process is repeated 20 times.

to bigTest
repeat 20 [
make "obj3 scale :obj2 1+(random 10)/10 1+(random 10)/10
make "obj3 rotz :obj3 random 360
make "obj3 trans :obj3 random 300 random 300
drawPos :obj3 ]
end

Download the full code for this exercise.

Last updated 23rd February 2010