Finding Squares |
|
This Logo program finds pairs of squares which total to the same number. You give it one number from each pair. The program uses two nested for loops to test all the integers from 1 to 99 paired with each start number. The program ignores the trivial case of pairing the start numbers.
to findsqs :a :b
make "sa :a*:a
make "sb :b*:b
for [n 1 99 1] [
for [m 1 99 1] [
make "s1 :n*:n+:sa
make "s2 :m*:m+:sb
if :s1=:s2 [
if not :a=:m [
print (list :a :n :b :m)
print (list :a*:a :n*:n :b*:b :m*:m)
print :s1
]] ]]
print "DONE
end
findsq.lgo Download the logocode. Load it into logo and type findsqs 26 49 etc. to get it to run.
|
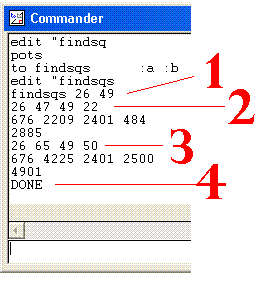
- This command sets the program off looking for two squares to pair with 26 and 49.
- This line shows the first solution found: 26 47 49 22.
- This line shows the second solution found: 26 65 49 50.
- The program prints done when it has searched all the way up to 100.
|
Finding Highest Common factors |
|
This program uses the Euclidean Algorithm to find the highest common factor (greatest common divisor) of two numbers.
The algorithm is very simple. If we have two numbers then the hcf of both must divide into the smaller number and the remainder left when the larger is divided by the smaller.
big = n.small + remainder
Thus we can reduce the problem to successively finding the hcf of the smaller number of the pair and the remainder left from dividing the smaller into the larger.
eg HCF 144 96
144 = 1*96 + 48
HCF 96 48
96 = 2*48
HCF of 144 & 96 is 48
to hcf :big :small
localmake "rem remainder :big :small
ifelse :rem=0 [(print [HCF is] :small)][
ifelse :rem=1 [(print [HCF is 1] )][hcf :small :rem]]
end
|
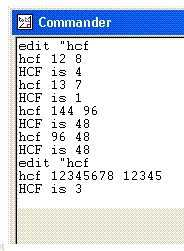
This program is an example of recursion. It starts by finding the remainder of big/small. If this remainder is 0 then small is a divisor of big and so small is the hcf. If not then the next check is to see if the remainder is 1. If this is the case then we have two numbers which are mutually prime. They have no divisor in common. If the remainder is neither 0 nor 1 then we repeat the process but with small and remainder instead of big and small. This provides the element of recursion in the definition of the procedure.
|
Testing for Primes
This procedure tests for primes. It is simple but not the most elegant solution in that it tests all odd numbers as trial factors.
It uses output to "return" an answer, prime or composite. This is a useful way to use procedures as it makes it much easier for procedures to call each other.
|
|
to pritest :number
localmake "fact :number
if (0=remainder :number 2) [
localmake "fact 2 ]
localmake "trial 3
if (0=remainder :number :trial) [
localmake "fact :trial
]
if (:fact=:number) [
do.until [
make "trial :trial+2
if (0=remainder :number :trial) [
localmake "fact :trial]
][:trial>sqrt :number]]
ifelse (:fact = :number) [
output "prime ][ output "composite]
end
Test the procedure with a command line call such as:
repeat 21 [show (sentence repcount+1 pritest repcount+1)]
|

|
The program sets up a variable called fact, for factor which is set equal to the number being tested. If any trial factor leaves remainder 0 on division into the target number then fact is changed.
Two and three are treated first and then the odd numbers are used. This is inefficient for big numbers but okay for numbers upto a million or so.
A do until loop runs until the square root of the target number is exceeded. If none of the numbers up to and including the square root divide the target number then it is a prime.
Output returns the answer prime or composite depending on whether or not a factor has been found.
|
|
Finding Prime Numbers
This program has two parts.
- trialfact this tries all the known primes to see if they divide into the current trial number.
- primes this is the controlling program which feeds trial numbers to trialfact and then adds new primes to the list of known primes.
|
primes
Limit is the upper search limit for finding primes; Logo can only cope up to 1000000000 anyhow.
The list of known primes is seeded with 2,3,5,7,11 and 13.
The first new trial number is set at 15; the first odd number above the biggest known prime.
The loop runs until the limit is exceeded. You must make sure that a do.until loop has a valid exit condition.
Prime sends the trial number and the current primelist to the trialfact procedure.
If the answer isn't -1 then a new prime has been found and it is added to the list.
New primes are printed as they are found and the final list is printed at the end.
to primes :limit
make "primelist (list 2 3 5 7 11 13)
make "trial 15
do.until [
make "answer trialfact :trial :primelist
if :answer>1 [
print :answer
make "primelist lput :answer :primelist ]
make "trial :trial + 2
make "answer -1
][:trial>:limit]
print :primelist
end
|
trialfact
This procedure uses recursion to try each known prime, in turn, as a potential divisor of the trial number.
If the a remainder 0 is found then this shows that the trial number divides by a known prime and so an answer of -1 is returned.
If the first number on the prime list doesn't work then the list is shortened by removing the first entry and the procedure is called again.
It is important to check that the list hasn't been exhausted. If the last known prime number won't divide trial then trial must be a new prime number. Trial is then sent back as the answer from the procedure.
to trialfact :trial :trylist
make "rem remainder :trial first :trylist
ifelse (:rem=0)[
make "ans -1][
ifelse (count :trylist)=1 [
ifelse (remainder :trial first :trylist)=0 [
make "ans -1][ make "ans :trial] ]
[make "ans trialfact :trial butfirst :trylist]]
output :ans
end
|
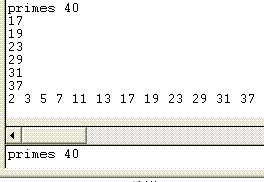
|

|
Factorising Numbers
|
|
This program has two parts.
- The top part divides the target number by 2 until a remainder is generated
- The second part then works its way up the odd numbers as trial divisors
The program could be improved by first generating a call to the prime number program and then using the prime list from that as the list of trial divisors. In practice, for small numbers it isn't worth the trouble. It could also be simplified by using recursion.
The do.until loops repeat until the limit of the square root of the target number is found.
If a remainder 0 is found then this indicates a succesful trial divisor. In this case the trial number is divided by this factor and the is process repeats.
As the trial divisors work up from 2 only prime factors will be generated.

|
factor
to factor :number
localmake "trial 2
do.until [
ifelse (0=remainder :number :trial) [
print :trial
make "number :number/:trial
][
make "trial 3
do.until [
ifelse (0=remainder :number :trial) [
print :trial
make "number :number/:trial
][
make "trial :trial+2
]
][:trial>sqrt :number]
]
][:trial>sqrt :number]
print :number
end
|





