Parametric equations in 2D and 3D.

Please note that this page is designed to help you practice parametric equations. This is not how you should draw shapes with Logo in either 2D or 3D. See the other Logo pages for the best ways into Logo graphics.

Aims and objectives.

Plot a sin wave on the xy plane and use basic Logo commands. Plot Lissajous' figures. More complex parametric equations in 2D. 3D parametric equations. Getting Started with Logo If you need it!

Drawing sin waves

Open the procedure editor by typing:

edit "drawsin

You are going to write a procedure which will plot a sin wave. If you want more help with procedures try the page in the LOGO basics section.

Type in this code (or cut and paste):

to drawsin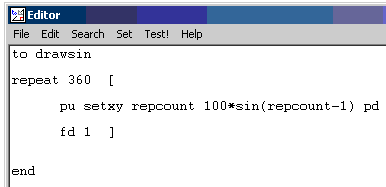
repeat 360 [
pu setxy repcount 100*sin(repcount-1) pd
fd 1 ]
end

Click save and exit in the file menu.

Run your code at the command line:

drawsin`

The drawing turtle starts from the xy coordinate origin which is located at thecentre of the screen. the x-axis is horizontal with positive values to the right. The y-axis is vertical with up positive.
pu lifts the drawing turtle and pd sets it down again.
setxy moves the turtle to the x y coordinates entered with the command. Thus setxy 100 100 sends the turtle from its current position to the point (100, 100).
repcount gives the current value of the repeat loop. Use the raw value for the x coordinate.
The y coordinate is given by sin(repcount) taken in degrees x100 to make it visible.

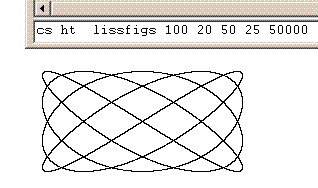
Lissajous' Figures

You are going to edit a routine called "lissfigs. Once you have programmed this routine into Logo you can then call it just like one of the normal Logo commands.

edit "lissfigs

Now edit the code so that it reads like this.

to lissfigs :a1 :av1 :a2 :av2 :plots
repeat :plots [
make "xCoord :a1*(sin :av1*(repcount-1)/500)
make "yCoord :a2*(sin :av2*(repcount-1)/500)
setxy :xCoord :yCoord
]
end

Now click on the "file" menu and select "save and exit".
The procedure receives 5 arguments:
:a1 x amplitude
:av1 x angular velocity
:a2 y amplitude
:av2 y angular velocity
plots - how many points to plot

Run the code from the command line with:

cs ht lissfigs 100 20 50 25 50000

The program works by using one sin wave to control the x-motion and a second sin wave to control the y-motion. The shape generated depends on the two angular velocities used used. These will execute their LCM of cycles before the trace repeats itself.

repcount-1 is used as the control parameter (time) so that "time" starts from 0.
It is divided by 500 to give 500 plots per cycle of the sin wave. This gives a smooth curve.

You can extend to 3 dimensions using this procedure.

to lissfigs3D :a1 :av1 :a2 :av2 :a3 :av3 :plots
repeat :plots [
make "xCoord :a1*(sin :av1*(repcount-1)/500)
make "yCoord :a2*(sin :av2*(repcount-1)/500)
make "zCoord :a3*(sin :av3*(repcount-1)/500)
setxyz :xCoord :yCoord :zCoord
]
end

You enter 3D mode by typing perspective into the command line.

Circles and Ellipses

This is the code for an ellipse or circle.

to para2 :a1 :av1 :a2 :plots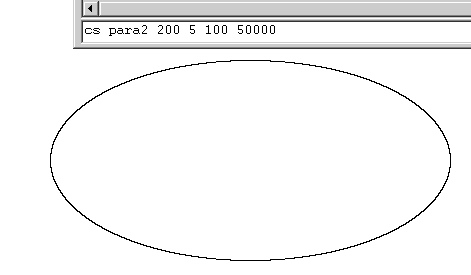
make "xCoord :a1*(sin 0)
make "yCoord :a2*(cos 0)
pu setxy :xCoord :yCoord pd
repeat :plots [
make "xCoord :a1*(sin :av1*(repcount-1)/500)
make "yCoord :a2*(cos :av1*(repcount-1)/500)
setxy :xCoord :yCoord
]
end

Complex Shapes

Ellipse modified by cosine function

to para3 :a1 :av1 :a2 :av2 :plots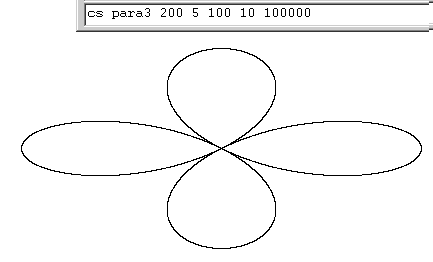
make "xCoord :a1*(sin 0)
make "yCoord :a2*(cos 0)
pu setxy :xCoord :yCoord pd
repeat :plots [
make "xCoord :a1*(sin :av1*(repcount-1)/500)*cos(:av2*(repcount-1)/500)
make "yCoord :a2*(cos :av1*(repcount-1)/500)*cos(:av2*(repcount-1)/500)
setxy :xCoord :yCoord
]
end

Cycloids

Two circular motions added together.

to cycloid :a1 :av1 :a2 :av2 :plots
make "xCoord :a1*(sin 0)+:a2*sin(0)
make "yCoord :a1*(cos 0)+:a2*cos(0)
pu setxy :xCoord :yCoord pd
repeat :plots [
make "xCoord :a1*(sin :av1*(repcount-1)/500)+:a2*sin(:av2*(repcount-1)/500)
make "yCoord :a1*(cos :av1*(repcount-1)/500)+:a2*cos(:av2*(repcount-1)/500)
setxy :xCoord :yCoord
]
end



Last updated 2nd February 2012